行测答题技巧：图形推理一笔画

　　“一笔画最短距离”，是近3年行测考试中出现的新题型，目前只在山东省考中出现过。由于这一类题将几何问题与图形推理中的一笔画问题相结合，比较新颖，很多考生对此束手无策，尤其是第一次遇到的同学，就算能得出正确答案，也要耗费大量时间。步知网(www.buzhi.com)讲解一下如何用一笔画来解题，希望给考生一些帮助。备考阶段，考生可通过《找准申论之道》系列花木君申论课程、《国考行测趋势分析》系列风暴羚羊行测课程、《面试的七大外功招式》系列北楚面试课程进行深入系统学习。

　　先读题：

　　一块由两个正三角形拼成的菱形土地ABCD周长为800米，土地周围和中间的道路如下图所示，其中DE、BF分别与AB和CD垂直。如要从该土地上任何一点出发走完每一段道路，问需要行进的距离最少是多少米?

　　A.1000+400√3

　　B.1100+400√3

　　C.1100+500√3

　　D.1000+600√3

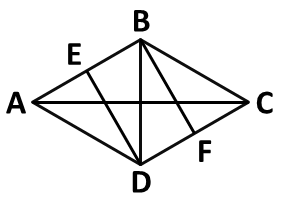
　　因为题干中要求必须走完每一条道路，那么，如果能够按照一笔画图形不走重复路线的话，行进距离肯定是最短的。

　　我们先回顾以下一笔画的相关知识：

　　1. 当奇点的个数为0或者2时，这个图形可以一笔画完成。

　　2. 当奇点的个数为0时，所有的点都是偶点，可以从任意点出发，完成一笔画并且回到原点。

　　3. 当奇点的个数为2时，必须从奇点出发，回到另外一个奇点，才能完成一笔画。

　　我们观察题中的图形，图中一共有4个奇点，分别是A、E、F、C，至少需要两笔画完成，为了方便确定最短路线，我们要想办法让它变为一笔画。

　　怎么变呢?可以将某些奇点连接起来，让这些奇点变为偶点，最终将图形中的奇点数变为0或2。

　　如下图所示，将图1的两个奇点连接，图形就转换成一笔画图形(图2)。

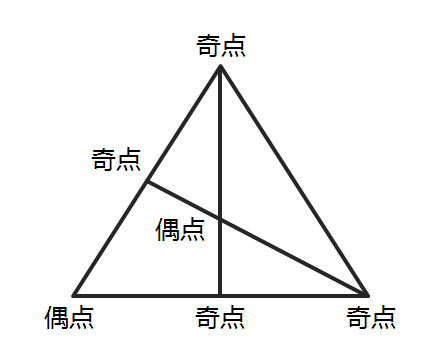
图1

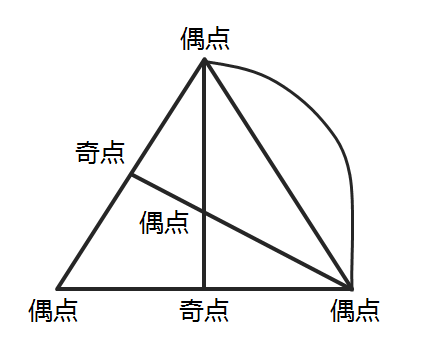
图2

　　难点就在于这条连接线的长度是多少呢?既然这条连接曲线是自行假设的，为了让它尽可能短，根据“两点之间线段最短”，不妨假设这条连接线的长度就是原来两个奇点的连接线(假设两点为A、B，连接线长度就是AB)，就相当于这条线段走2次。

　　这样，图1就变成了一笔画图形，图中所有路段都可以一笔走完。但要使得总路程最短，就应该选择相邻最近的两个奇点变成偶点(假设两点为B、C)，如图3，行走的最短距离=图1中原有线段的长度之和+BC。

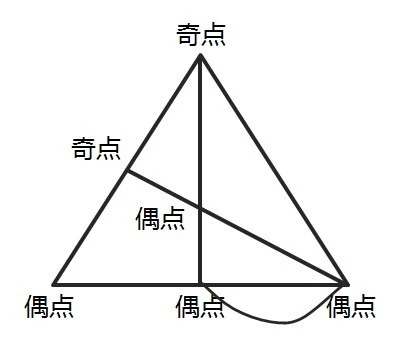
图3

　　回到题目，观察可知连接两个奇点最短的距离是AE或者CF，为100米，则最短路程就是所有线段之和再加上AE或者CF的距离，S=800+200(BD的长)+4×100√3(4条正三角形的高)+100(多走的AE)=1100+400√3，正确答案为B。