逻辑判断：三段论规则

　　今天跟大家分享逻辑判断中一个核心考点--三段论规则。三段论是演绎推理的基础形式，也是行测的一个传统考点。同学们往往喜欢画“圈圈”去做，速度慢，又极容易做错。其实，根据三段论本身蕴含的规则就可以快速解答，省时省力。

　　对于三段论规则，“爆发篇：核心考点精析”这一阶段中有一个具体的课时，整个课程内容大概是三个方面，如图所示：

　　一、三段论

　　三段论是一种推理形式，是两个直言命题作为条件，推出一个新的直言命题作为结论的推理。下图中的推理就是一个典型的三段论：

　　从形式上来说和，三段论就是两个直言命题推出另一个直言命题。但并不是任何两个直言命题推出另外一个直言命题的推理都是正确的三段论，正确的三段论只有四种基本形式，其中每一种均可用文氏图证明，如下图所示：

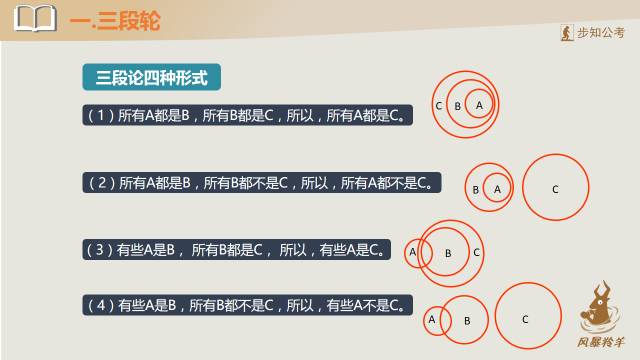
　　需要注意的是全称否定命题的两个概念，位置是可以互换的，比如“所有B都不是C”与“所有C都不是B”等价，都表示B和C是全异关系，所以比如第(4)种也可以写成“有些A是B，所有C都不是B，所以，有些A不是C”，意思一样。

　　二、三段论规则

　　分析三段论的四种形式，可以总结出四条规则，如图所示：

　　1. 全肯必肯，指两个条件是肯定命题，结论一定也是肯定命题，比如第(1)和第(3)种形式。

　　2. 一特必特，指条件中有一个是特称命题，结论一定是特称命题，比如第(3)和第(4)种形式。不可全特，指没有两个条件都是特称命题的，两个特称命题不能推出任何结论。

　　3. 一否必否，指条件中有一个是否定命题，结论一定是否定命题，比如第(2)和第(4)种形式。不可全否，指没有两个条件都是否定命题的，两个否定命题不能推出任何结论。

　　4. 中项，是指在条件中出现了两次，在结论中不出现的概念，在上述四个三段论中，中项都是“B”。B在条件中至少被全称或者否定一次。在上述四个三段论中，中项都被全称了一次。如果把“所有B都不是C”写成“所有C都不是B”，那么中项就被否定了。

　　三、例题讲解

　　此题需要补充一个条件保证三段论成立。给出的条件是特称命题，根据“不可全特”的规则，补充的条件不能再是特称命题，据此排除BCD，故答案为A。

　　此题跟上一题一样，给出的条件也是特称命题，但是只能排除掉CD。AB都是肯定命题，不能根据规则1和3进行排除。考虑规则4。中项是“高校教师”，在所给的条件中没有被全称也没有被否定，A项中没有被全称也没有被否定，B项中被全称了，所以选B。

　　题干给了三个直言命题，问推不出哪一项。

　　我们知道任何两个直言命题都有可能推出一个结论，所以如果直接推理，会比较麻烦。观察这三个直言命题，都是肯定命题，根据“全肯必肯”的规则，所推出的必须是肯定命题，选项中只有A项是否定命题，所以答案选A。