行测答题技巧：搞定这类“变态”图推题

　　这是一道真题，我知道你可能不服，先做做吧：

解析在这：

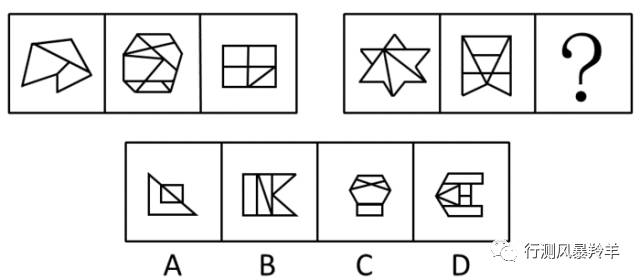
　　观察所给图形，可以视为被拆分成若干个不同的三角形和四边形。先分开数一下它们各自的数量。

　　第一组图形中，三角形的数量分别为1、4、2，四边形的数量分别为2、5、3，两者之间的差为1。

　　第二组图形中，三角形的数量分别为2、3、?，四边形的数量分别为3、4、?，前两个图形的差均为1，因此问号图形的四边形数量应比三角形数量多1。

　　故答案为D。

　　看懂了么?先别抱怨，这类题目，在行测考试中出现过多次!

　　我们都知道，行测是考思维的题目，在基本考点的基础上，可以无限拓展和延伸，说行测是最灵活的考试，绝不为过。

　　如果一种考法考过三四次，就说明被多个命题人认同，就有再考的可能性，我们就要接受这种考法，并去掌握。

　　提炼一下，这种考法是：每个图形被分割成若干个多边形，它们之间有某种数量关系。可以是都分成一种图形，比如都分成三角形，也可以是分成两种图形，比如这个题。不太可能分割成三种，太复杂，太耗费时间。

　　这种题的难点是怎么数，是只数被分割成一个封闭区域的多边形，还是说多个封闭区域组成的多边形也要数。也就是有些小伙伴提到的只数小的，还是大的也一起数?

　　从出现过的题目看，两种考法都出现过。我们并不能从图形特征上去判断是哪一种，只能一种一种去试，看看哪一种有规律。

　　另外需要注意的是，如果分割成两种图形，一定要分开数。数完后，如果每一种图形单独构不成规律，再看和、差的数量规律。

查看更多图推解题思路，行测答题技巧>>