数学运算之最短路线数求法--标数法

　　很多同学都有些畏惧“数学运算”，在考场中，甚至会直接放弃，然“数学运算”其实是拉开分差的关键。严格来说，“数学运算”中有很多题目在掌握一些核心考点和技巧方法后，是很容易拿分的。文章内容由步知公考风暴羚羊老师提供，可免费试听羚羊老师课程。

　　我在7月31日的公考课中(现在有回看)，就有谈到“数学运算”中最短路线数的技巧方法。我这里再详细说明一下。

　　什么是求最短路线数的问题呢?如下题：

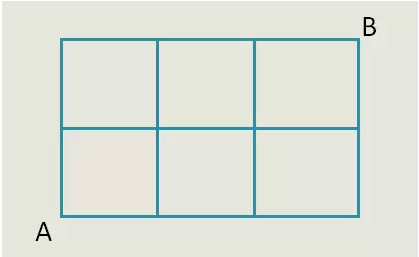
　　下图中的线段表示的是汽车所能经过的所有马路，这辆汽车从A走到B处共有多少条最短路线?

　　说解法前，先来看看这个最短路线怎么确定?

　　从A到B要最短，至少要走过三条横向马路，两条纵向马路，因此需要走5步(如下图，这是其中一种走法)。注意，每一步的方向都是由A向B移动，即往右走和往上走，不走回头路，那么，才会形成最短路线，其中，满足5步的路线非常多条，如何确定它的具体数量?

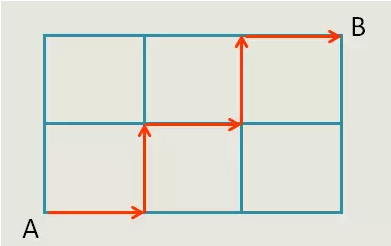
　　要算出数量有两种解法，一种简单粗暴，名为“标数法”;一种逻辑严谨、高大上，名为“排列组合”。

　　本文先教大家怎么用简单粗暴的标数法。下一次记会继续分享利用排列组合的知识更为快速的解法。

　　标数法，简单明了。从距离A 近的点开始，算出从A点到每一点的最短路线的数量a，从而，最后算出到B点的数量。具体解题步骤如下：

　　1、先算与A相邻的点(如下图，C和D)的最短路线的数量，毋庸置疑，数量自然是1，标注在相应点上。

　　2、计算与已得出数量的点相邻的下一个点，即E、F、H三点。你会发现，从A到这三点，要走最短路线，就只能是向右走或向上走，那么必须要先走AC或AD，因此，去往这三条的路线数就依赖于C和D这两点。A到E，只能经过C，所以，到E的最短路线数量=到C的数量=1;同理，可得从A到H点的最短路线数量=到D的数量=1。A到F，由于F点相邻的点有C和D两点，所以从这两个方向都是最短路线，那么，到F点的最短路线的数量=到C点的+到D点的=1+1=2。

　　3、继续选择与已得出数量的点相邻的下一个点，如G点。到G点的最短路线数=到F点的+到H点的=2+1=3。同理可得剩余所有点的最短路线数。具体数量如下图。

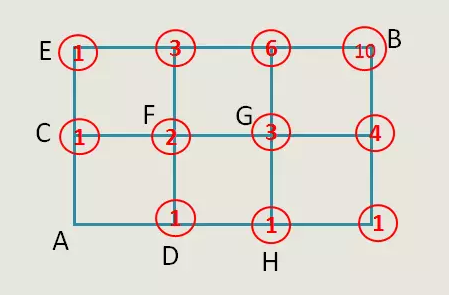
(PS：注意数量为6的这个点，切记不要算漏了)

　　4、最后，算出B点的数为10。因此从A点到B点的最短路线数量=10条。

　　为了便于大家记忆，不搞混。这里可以借用对角线来辅助解题。如下图，画出对角线后，对角线上两点的数量和=靠近B点的直角上的点的数量。这样子就不用担心会有遗漏。

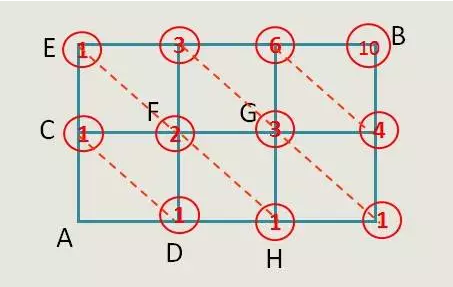
　　标数法的实质是列举法，通过累加的方式求出列举的所有情况数，原理虽粗暴，但简单实用。

　　下面我们来做一道题，练一练。

　　从A地到B地的道路如图所示，所有转弯均为直角，问如果要以最短路线到达B地，有多少种不同的走法?

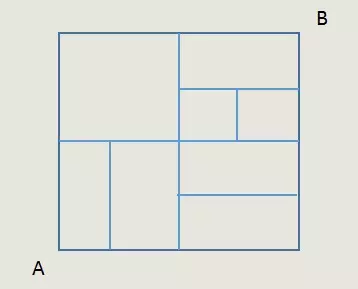
　　PS：最近有不少参加事业单位的同学反映试卷中出现了我讲到的原题。为此，参加事业单位考试的同学请务必弄懂我课程中讲到的每一道题目，以及每一堂课的课后练习题。

　　本文为步知网原创文章，任何公司、媒体、网站或个人未经授权不得转载、链接、转贴或以其他方式使用。已授权许可的媒体、网站，在使用时必须注明"稿件来源：步知网"，违者本网站将依法追究责任。