学会套用排列组合，10秒搞定最短路线数题！

时间：01-21|来源：步知资讯|阅读：

分享|打印|下载此文章|放大字号|缩小字号

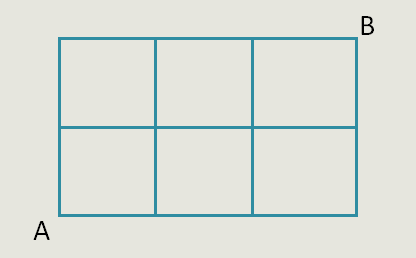
　　下图中的线段表示的是汽车所能经过的所有马路，这辆汽车从A走到B处共有多少条最短路线?

　　说解法前，先来看看这个最短路线怎么确定?

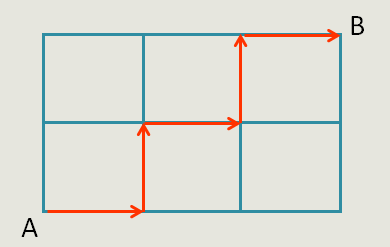
　　从A到B要最短，至少要走过三条横向马路，两条纵向马路，因此需要走5步(如图)。注意，每一步的方向都是由A向B移动，即往右走和往上走，不走回头路，那么，才会形成最短路线，其中，满足5步的路线非常多条，如何确定它的具体数量?

　　要算出数量有两种解法，一种简单粗暴，名为“标数法”;一种逻辑严谨、高大上，名为“排列组合”。本文主要分析高大上但速度快的排列组合法。

思路1：分类原理

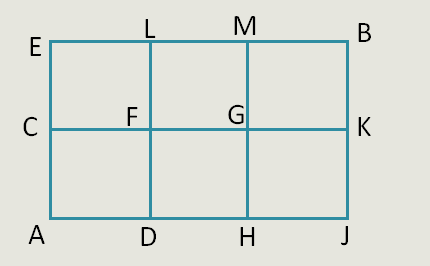
　　我们知道，只要确定了A到B的纵向上是走的哪2条马路，就能确定最短路线的数量。但这2条纵向马路不能是随机从现有的8条中选出2条。如上图，如果不巧选了DF和CE，那么，整体的路线是AD—>DF—>FC—>CE—>EL—>LM—>MB(共7步>5步)，由于其中走了DF—>FC这段回头路，所以路线就变为了7步，显然不是最短路线。

　　所以，根据实际情况，最短路线的数量需要分类考虑：

　　1) 纵向路线，下方选择AC，那么，第二条纵向马路可以是上方四条中任意一条，共4种最短路线。

　　2) 纵向路线，下方选择DF，那么，第二条纵向马路只能选择FL、GM、KB中一条，共3种。

　　3) 纵向路线，下方选择HG，那么，第二条纵向马路只能选择GM、KB中一条，共2种。

　　4) 纵向路线，下方选择JK，那么，第二条纵向马路只能选择KB，1种。

　　分类用加法，四类情况一共有4+3+2+1=10种。

（点击学习更多行测快速解题技巧）

思路2：分析最短路线的情况，直接用公式

　　根据“从A到B要最短，至少要走过三条横向马路，两条纵向马路”和“只要确定了A到B的纵向上是走的哪2条马路，就能确定最短路线的数量”，以及，每条纵向马路都与一条横向马路相连，那么，如果将“每一条横向马路我们看成与之右侧相邻的一条纵向马路”，就可得：从3+2=5条马路中选出2条马路，有多少种选法就有多少种最短路线，共C(5,2)=5×4/2=10种。

　　这里大家最疑惑的是，为什么选择一条横向和一条纵向也可以确定最短路线呢?关键在前面说的一句话：“每一条横向马路我们看成与之右侧相邻的一条纵向马路”，此时，我们抽取的每一条横向马路其实意味着的都是选择了某一条纵向马路，因此，一共是选择两条纵向马路，而这两条纵向马路会遵循“上方所说的分类原理”中的规律。具体为什么，我们通过示意图来演示。

　　由于三条横向马路分别代表是不同的步，我用a、b、c表示这三步，两条纵向马路我用d、e表示。

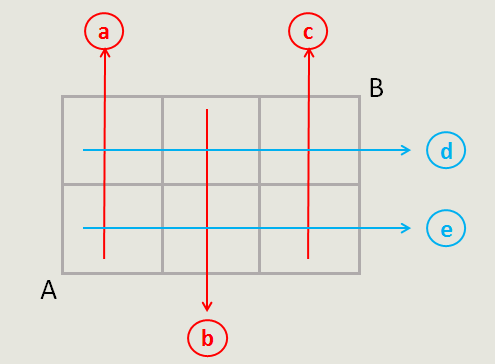
　　一、那么，当选出a和d，代表的路线如图，a此时指a方位的最底端的横向马路。(为什么是这样，因为有d在，此时a代表是下方的某一条纵向马路，即它右端的纵向马路，上方的是与它相连的纵向马路)

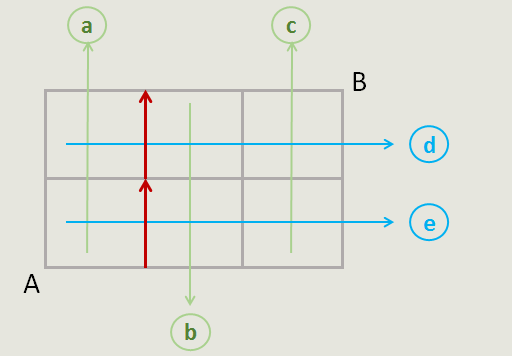
　　同理，若选择c和d，路线如图：

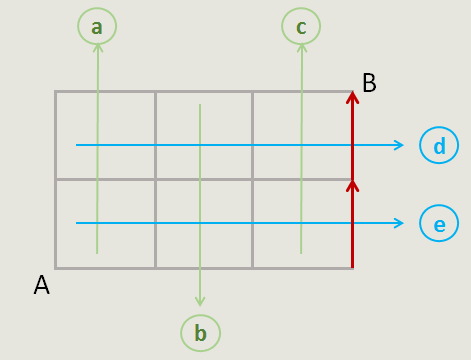
　　(同理可得选择b和d的路线图，这里暂不演示，同学们自己画一画)

　　二、选出a和e，代表的路线如图，a此时指a方位的中间位置的横向马路。同理可得选b和e 、或选c和e对应的路线。(为什么是这样，因为有e在，此时a代表是上方的它右侧的纵向马路，e是它下方与它左边相连的纵向马路)

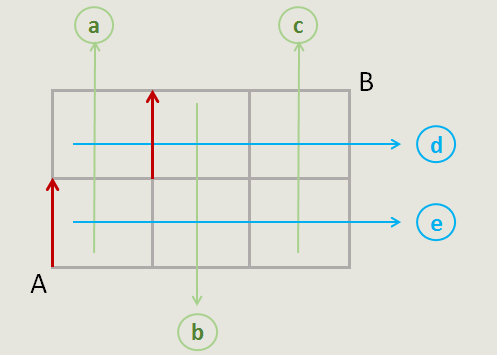
　　(选b和e 、选c和e对应的路线，同学们自己画一画)

　　三、选出a和b，代表路线如图，靠近A的a选择a方位底端的马路(代表它右侧的纵向马路)。靠近B的b选择b方位中间的马路(代表它右侧的纵向马路)。从而确定一种最短路线的走法。

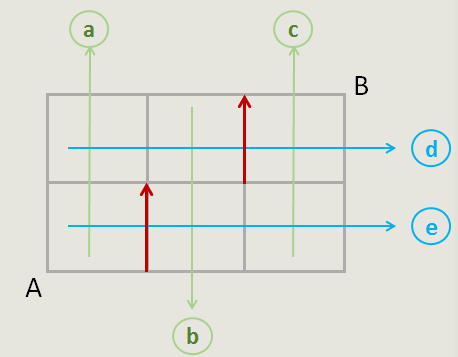
　　同理，若选择a、c，路线如图：

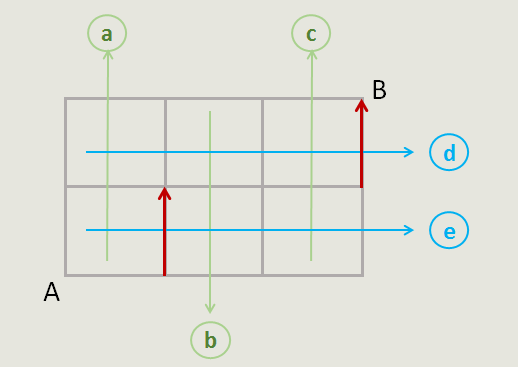
　　同理，若选择b、c，路线如图：

　　四、若选择d和e，即不走a、b、c三个方位的底端或中间位置的任一条横向马路。直接从连接A点的左侧经过。

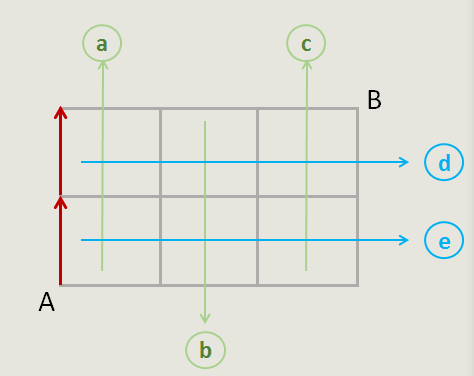
　　这样子把四大类的示意图一画，大家就清楚为什么“C(5,2)”就能求出所有的最短路线数，所以下次再用“排列组合公式”求最短路线数时，千万不要再怀疑自己书写的组合式子中的n、m到底对不对，只要原理对，那你就能做对。当然，这里要提醒一下，排列组合只适合求解这种规则的田字格式样的路线图的最短路线数，像之前的标数法求最短路线数的文中最后一道例题就不适合用排列组合公式。

　　练习环节：

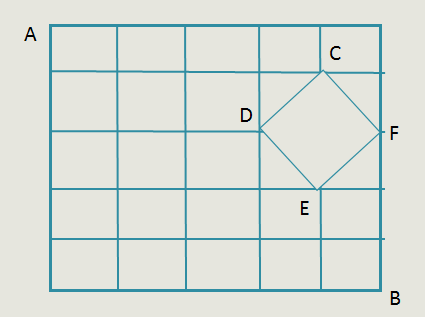
　　如下图所示，某镇共有6条东西方向的街道和6首南北方向的街道，其中有一个湖，街道在此变成一个菱形的环湖大道。现要从城镇的A处送一份加急信件到B处，为节省时间，要选择最短的路线，共有(　)种不同走法。