行测答题技巧：补补逻辑判断数量题的基础知识

　　行测很多题目都是根据中学的数学知识演化而来，补好中学基础才能获取!为此，我们的VIP课程体系刻意设置了【基础篇：中小学基础知识回顾】，其目的就在于帮大家再打打基础。

　　关于今天的分享，我们先做做这道题：

　　出席某学术会议的有5人是书法爱好者，4人是南方人，2人是福建人，3人是人大代表。以上叙述涉及了所有会议参加者，其中福建人不爱好书法。

　　那么，参加会议的人数是( )。

　　A. 最多14人，最少5人

　　B. 最多14人，最少7人

　　C. 最多12人，最少5人

　　D. 最多12人，最少7人

　　一起来看看解析：

　　本题考查逻辑判断中的数量题。

　　题干中主要涉及书法爱好者、南方人、福建人和人大代表四个概念。要使参加会议的人数尽可能多，则概念之间尽可能是全异关系，但福建人一定真包含于南方人，所以最多应为5+4+3=12人。

　　最少即概念之间尽可能互相重合，于是3个人大代表和4个南方人可以包含于书法爱好者中，但是福建人不爱好书法，则2个福建人与书法爱者是全异关系，不可能互相重合，所以最少应为5+2=7人。故答案选D。

　　读完解析，不由感慨一句，这是逻辑题吗?全同、全异、包含、真包含，这不是高中所学的集合知识吗? 是的，这些是高中的数学知识，但一样可以解答很重视逻辑思维的逻辑题。具体思路如下：

　　一、用集合来表示题干条件

　　“5人是书法爱好者，4人是南方人，2人是福建人，3人是人大代表”即

　　集合A：5个书法爱好者

　　集合B：4个南方人

　　集合C：2个福建人

　　集合D：3个人大代表

　　明显，福建人肯定都是南方人，即C中的元素都属于B，且B中有不是福建人的，可知，C真包含于B，如图1。说明，B集合中的4个元素有2个来自C集合，即B和C的元素个数之和=4。

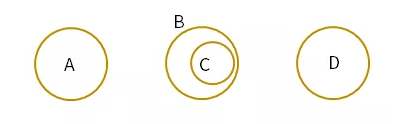
(图1)

　　“福建人不爱好书法”用集合表示，如图2。

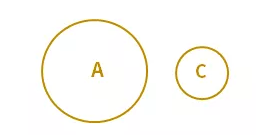
(图2)

　　二、分析题目

　　“参加会议的人数最多”即四个集合的元素之和要最多，显然，如图1所示，就是元素数量最多，共5+4+3=12个。即最多有12人参加会议。

　　“参加会议的人数最少”即四个集合的元素之和要最少。那么，A、B、D集合之间有没有可能重合呢?

　　当然是可能的，而且是重合得越多，自然多个集合的元素总个数越少，如图3所示，元素数量只有A中的5个和C中的2个是不重合的，其他都和A或C重合了。

　　因此，元素总数一共是5+2=7个。即最少有7人参加会议。

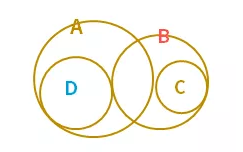
　　三、回顾下高中的集合知识点。

　　1、集合

　　由一个或多个确定的元素所构成的整体叫做集合。若x是集合A的元素，则记作x∈A。

　　2、集合中的元素有三个特征

　　1)确定性(集合中的元素必须是确定的)。

　　2)互异性(集合中的元素互不相同)。例如：集合A={1，a}，则a不能等于1)。

　　3)无序性(集合中的元素没有先后之分)，如集合{3,4,5}和{3,5,4}算作同一个集合。

　　3、集合间的基本关系

　　1)相等：集合A与集合B中的所有元素都相同。也可以表述为A和B全同。

　　2)不相等：集合A与集合B中的所有元素都不相同。也可以表述为A和B全异。

　　3)子集：A中任一元素均为B的元素，称集合A是集合B的子集。也可以表述为A包含于B。

　　4)真子集：A中任一元素均为B的元素，且B中至少有一元素不是A的元素，称集合A是集合B的真子集。也可以表述为A真包含于B。

　　5)交集和并集

　　①两个集合的交集：A∩B

　　一般地，由属于集合A且属于集合B的元素所组成的集合，叫做集合A与B的交集 。记作：A∩B， 读作：“A交B”， 即： A∩B={x|∈A，且x∈B} 。

　　说明：两个集合求交集，结果还是一个集合，是由集合A与B的公共元素组成的集合。

　　②两个集合的并集： A∪B

　　一般地，由所有属于集合A或属于集合B的元素所组成的集合，称为集合A与B的并集记作：A∪B，读作：“A并B”，即：A∪B={x|x∈A，或x∈B} 。

　　说明：两个集合求并集，结果还是一个集合，是由集合A与B的所有元素组成的集合

　　【备注：重复元素只看成一个元素】

点击查看更多风暴羚羊的真题详细解析，学习行测快速答题技巧>>