2016年公务员考试资料分析答题技巧：数据计算技巧知识点储备

　　一、尾数法

　　尾数法主要指通过运算结果的末位数字来确定选项，因此若选项中末尾一位或者几位各不相同，可以通过尾数法判断答案。在资料分析中常用于和、差的计算，偶尔用于乘积的计算。尾数可以指结果的最末一位或者几位数字。

　　1.加法中的尾数法

　　两个数相加，和的尾数是由一个加数的尾数加上另一个加数的尾数得到的。示例：2452+613=3065，和的尾数5是由一个加数的尾数2再加上另一个加数的尾数3得到的。

　　2.减法中的尾数法

　　两个数相减，差的尾数是由被减数的尾数减去减数的尾数得到的，当不够减时，要先借位，再相减。

　　示例：2452-613=1839，差的尾数9是由被减数的尾数2借位后再减去减数的尾数3得到的。

　　3.乘法中的尾数法

　　两个整数相乘，如果积的所有有效数字都保留，那么积的尾数是由一个乘数的尾数乘以另一个乘数的尾数得到的。

　　示例：2452×613=1503076，积的尾数6是由一个乘数的尾数2乘以另一个乘数的尾数3得到的。

　　二、首数法

　　首数法与尾数法类似，是通过运算结果的首位数字或前两、三位数字来确定选项的一种方法。除适用于选项中首位数字或前几位数字各不相同的情况外，还可用于分数的大小比较，如各分数的分子、分母位数相同，可根据化为小数时的首数大小找出最大和最小的分数。首数法一般运用于加、减、除法中，在除法运算中最常用。

　　1.加法中的首数法

　　两个数相加，如果两个数的位数相同，和的首数是由一个加数的首数加上另一个加数的首数得到的，但还要考虑首位后面的数相加后是否能进位;两个数的位数不同时，和的首数与较大的加数一致或者为较大的加数的首数加1。

　　示例：3288+2216，百位没有进位，和的首数为3+2=5，首数为5;

　　3888+2716，百位有进位，和的首数为3+1+2=6，首数为6。

　　2.减法中的首数法

　　两个数相减，如果两个数的位数相同，差的首数是被减数的首数减去减数的首数得到的，但还要考虑被减数首位后面的数是否需要借位。两个数的位数不同时，差的首数与较大的数一致或者是较大的数的首数减1(借位时)。

　　示例：3888-216，被减数百位数字作差时不需要借位，则差的首数与较大的数3888首数一致，首数为3;

　　5288-2316，被减数的百位数字作差时需要借位，则差的首数为5-1-2=2，首数为2。

　　3.除法中的首数法

　　被除数除以除数时，先得到商的高位数，除法进行到可以判断正确选项为止。

　　示例：3888÷216，商的首数等于3888÷216=1X，首数为1。

　　三、取整法

　　取整法指在计算多位有效数字的数据时，可将其个位、十位或百位等的数据根据具体情况进行进舍位，得到相对简单的数据，再进行计算的方法。取整法可用于加减乘除四则运算中，取整时可以根据数值特点进行四舍五入。

　　【例题1】 2003-2007年SCI(科学引文索引)收录中国科技论文情况

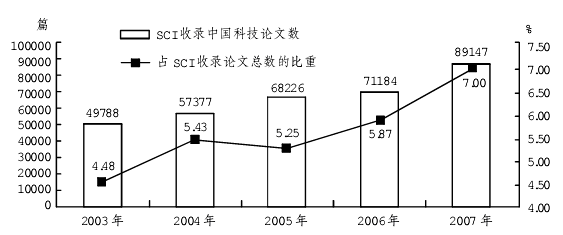
　　2003-2007年，SCI平均每年约收录多少篇中国科技论文?

　　A.5.9万 B.6.3万 C.6.7万 D.7.1万

　　解析：此题答案为C。2003-2007年，SCI平均每年收录的中国科技论文为(49788+57377+68226+71184+89147)÷5≈(50000+60000+70000+70000+90000)÷5=68000=6.8万篇，最接近的选项为C。

　　四、特征数字法

　　特征数字法是利用一些常用数据的数学特征，将百分数、分数、小数、整数等进行相互转化的化简方法。用特征数字来代替原来复杂数字，可以有效地减少计算量。特征数字法中主要有以下几类常见的特殊数字。

　　1.当分式中出现尾数为5、25、125的数据时，可以将分子分母同时乘以2、4、8，使得分子或分母的有效计算数位减少、计算量减轻。

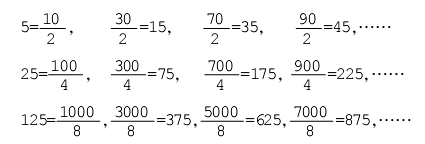
　　2.当算式中的百分数、小数接近下列真分数时，可以化成近似的真分数，再进行计算。

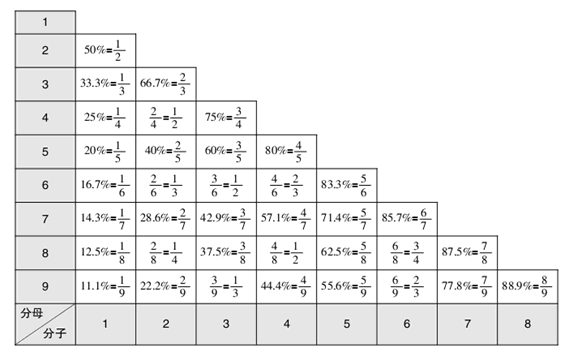
　　3.当算式中的小数为以下情形时，可以化成相近部分无理数，再进行计算。

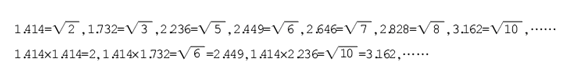
　　【例题2】 2010年1～3月，法国货物贸易进出口总额为2734.4亿美元，同比增长13.4%。其中，出口1264.7亿美元，同比增长14.5%;进口1469.7亿美元，同比增长12.4%;逆差205.0亿美元，同比增长1.0%。

　　2010年1～3月，法国货物贸易出口额比上年同期增长了约多少?

　　A.120亿美元 B.140亿美元

　　C.160亿美元 D.180亿美元

　　五、范围限定法

　　范围限定法是指通过对计算式中数据进行放大或缩小，将计算式的数值限定在一定范围内，再通过选项或其他限定条件来选择正确选项或进行大小比较。

　　当计算或比较若干个数值的大小时，如果选项间的差距较大，可以采用范围限定法，并要注意放缩的一致性。

　　1.加法\乘法运算

　　放大(缩小)其中的一项会使结果相应放大(缩小)。

　　示例：A、B、C、D为四个正数，且A>C>B>D。则A+B>C+B>C+D;A×B>C×B>C×D。

　　2.减法运算

　　被减数放大(缩小)导致结果相应放大(缩小)，减数放大(缩小)导致结果相应缩小(放大)。

　　示例：A、B、C、D为四个正数，且A>C>B>D。则A-D>C-D>B-D;A-C>A-B>A-D。

　　3.除法运算

　　被除数放大(缩小)导致结果相应放大(缩小)，除数放大(缩小)导致结果相应缩小(放大)。

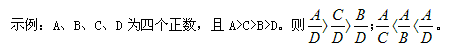
　　精华推荐

　　2017年国考行测必考常识汇总

　　2017年国家公务员考试行测模拟卷汇总

　　步知公考申论花木君、行测风暴羚羊视频课程合集

　　2017年国家公务员考试备考资料合集（行测+申论）