2017年国考资料分析答题技巧：如何计算平均量的增长率

　　在资料分析的平均量这个概念中，平均量的增长率是重点也是难点。这一考点的之所以难，是因为很多同学在学习的过程中容易将其与比重的变化混淆。下面老师就带领大家来见识一下平均量的增长率这一概念的真面目。

　　一、平均量

　　二、平均量的变化

　　平均量的变化主要有两个考点。一是判断平均量的变化，二是计算平均量的增长率。平均量的变化较比重的变化而言，判断的方法是相类似的，主要区别在于计算。

　　(一)判断平均量的变化

　　总量增长率>份数增长率，平均量增加;

　　总量增长率<份数增长率，平均量减少;

　　总量增长率=份数增长率，平均量不变。

　　(二)计算平均量的增长率

　　比重是百分数，是一个相对量。比重的变化是由比重作差得来的，结果为：

　　(注：增长率的差值为部分增长率与整体增长率的差值)

　　而平均量是一个绝对量。平均量的增长率只能通过“

　　”来求，而不是通过作差来求，因此计算式是不相同的。

　　在这个式子本身是带有符号的。当总量的增长率>份数的增长率时，平均量的增长率为正，即平均量增加;当总量的增长率<份数的增长率时，平均量的增长率为负，即平均量减少。这与之前判断平均量的变化是一致的，有所重复。为了方便大家记忆，我们可以将公式写为：

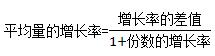
　　(注：增长率的差值即为总量的增长率与份数增长率的差值)

　　【例】全国2007年认定登记的技术合同共计220868项，同比增长7%;总成交金额2226亿元，同比增长22.44%;平均每项技术合同成交金额突破百万元大关，达到100.78万元。问：2007年，平均每项技术合同成交金额与上年相比：

　　A.增长了14.43% B.增长了16.44%

　　C.减少了14.43% D.减少了16.44%

　　【答案】A。中公解析：本题考查的是平均量的变化。首先判断平均量的变化，2007年总成交金额同比增长22.44%，大于认定登记的技术合同数量同比增长7%，即总量增长率小于份数增长率，平均量增加，排除C、D。其次计算平均量的增长率，即

　　对于平均量的变化这部分内容，判断变化比较容易，关键是要准确记忆平均量增长率的公式。在做此类题目时，首先，我们通过比较增长率的大小即可判断平均量增加还是减少;其次，直接代入平均量增长率的公式进行求解即可。