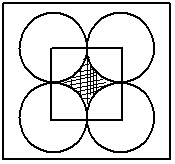
1.如图,半径为1的四个圆两两相切,求图中阴影部分的面积(π=3.14)?( )
A. 0.86
B. 1.86
C. 2.32
D. 3.86
2. 甲单位义务植树一公里,乙单位紧靠甲单位又植树一公里,如果按10米植一棵树的话,两单位共植树多少棵?( )
A. 199
B. 200
C. 201
D. 202
3. 有a、b、c三个数,已知a×b=24,a×c=36,b×c=54,求a+b+c=( )
A. 23
B. 21
C. 19
D. 17
4. 50个数1,2,3,2,3,4,3,4,5,4,5,6,5,6,7,6,7,8,…的和是( )
A. 568
B. 497
C. 523
D. 491
5. 一次数学考试满分是100分,某班前六名同学的平均得分是95分,排名第六的同学的得分是86分,假如每人得分是互不相同的整数,那么排名第三的同学最少得多少分?
A. 94
B. 97
C. 95
D. 96
答案及详细解析
1. 解析: 此题属于几何问题。考察扇形面积的计算;相切两圆的性质;几何图形的割补平移。本题的解题关键是能看出阴影部分的面积为边长为2的正方形面积减去4个扇形的面积(一个圆的面积).阴影部分的面积=(2×2)-(π×1²)=4-π=0.86。故答案为A。
2. 解析: 本题考查植树问题。甲单位在一公里内植树,则两端都可以种一棵树,则一共可以种1000÷10+1=101棵树;乙单位紧靠着甲单位植树,则有一端不需要植树,一共可以种1000÷10=100棵树。甲、乙共植树101+100=201棵树;故答案为C。
3. 解析: 由ab=24,ac=36得,2c=3b,又bc=54,解方程得b=6,c=9。故得a=4,所以a+b+c=19。故答案为C。
4. 解析: 本题属于计算问题。这50个数三个一组可以分成17组:(1,2,3),(2,3,4),…,(16,17,18),(17,18)。每组都是连续的自然 数。注意第17组只有两个数。前16组中,每一组三数之和都比前一组大3,因此这16个和构成首项为6,公差为3的等差数列,数列的和456。再加上第 17组的和35,则这50个数的和为491。故答案为D。
5. 解析: 六名同学得分总和为95×6=570分,要使第三名同学得分最少,则其他人得分要尽可能的多,因此第一和第二名得分分别为100和99分,第六名得分为 86分,则三、四、五名同学得分总和为570-285=285分,此三名同学平均分为95分,则,第三名同学最少需得到96分。(或者:因为第六人得分 86,比平均分低9分,故其他5人有9分进行分配,第一第二名分别是100和99分,即,9分全部分配完,其他三人平均分95,第五名拿1分给第三名,即 96分。)。故答案为D。
