行测真题之数量关系典型例题精讲（11）

1、-2，-1，2，-2，（ ），8。
A. 1
B. -1
C. 4
D. -4

解析： 分析题目发现，-2×（-1）=2，-1×2=-2即第一、二项之积等于第三项，，所以2×（-2）=-4；验证（-2）×（-4）=8，因此，本题答案为D。

2、2246，3164，5180，6215，（ ）。
A. 5711
B. 7132
C. 8591
D. 9125

解析： 此数列数位相同、大小变化紊乱，属于组合拆分数列的特征，尝试拆分无明显规律，只能是数位组合，数列中各个数的数位之和=14，只有A选项符合。因此，本题答案为A。

3、13/48，14/59，17/81，32/125，（ ）。
A. 49/213
B. 50/219
C. 50/239
D. 49/239

解析： 分数数列一般考察分子分母单独成规律，或者分子分母交叉成规律，我们解答此类推理题目一般采用的是上下看，左右看，上下交叉，没明显规律，则单独看分子分 母，分子无明显规律，分母相邻两项做差分别为11,22,44，（88）呈明显等比数列，易知下一项的分母为：88+125=213，因此，本题答案为 A。

4、11，14，12，20，13，30， （ ），44，15，（ ）。
A. 1555
B. 1460
C. 1462
D. 1560

解析： 此数列项数＞8、有2括号，属于组合拆分数列中交叉、分组数列明显特征。 发现分组无规律，属于交叉数列，奇数项为等差数列11、12、13、（14）、15；偶数项为14、20、30、44、（ ），相邻两项相减 为：6,10，14，（18），为公差是4的等差数列，所以偶数项最后一项=44+18=62。因此，本题答案为C。

5、226，197，170， （ ），122。
A. 100
B. 145
C. 125
D. 123

解析： 观察数字，整体趋势为变小，且幅度小，平稳，但是未知项在中间，而不是两 端，此类题目，我们一般采用数列试错，即：做差后先按照一种思想假设，之后反推到题目中进行验证，做差后，我们得：29，27，（），（），我们假设此时 的数列为等差数列29，27，25，23，170-25=145，验证：145-23=122，因此，本题答案为B。

6、小强从学校出发赶往首都机场乘坐飞机回老家，若坐平均速度40千米/小时的机场大巴，则飞机起飞时他距机场还有12公里；如果坐出租车，车速50千米/小时，他能够先于起飞时间24分钟到达，则学校距离机场（ ）公里。
A. 100
B. 132
C. 140
D. 160

解析： 设学校距离机场为X公里，则小强坐机场大巴距机场12公里所花时间T1=（S-12）/40；小强坐出租车到机场所花时间T2=S/50，由题意可得： T1=T2+24/60→（S-12）/40=T2=S/50+24/60→S=140。因此，本题答案为C。

7、某单位组织员工外出活动，所有员工刚好坐满10辆客车。已知大客车每辆乘坐50人，小客车每辆车坐30人，大客车比小客车一共多做了260人。则大客车有（ ）辆。
A. 3
B. 4
C. 6
D. 7

解析： 设大客车有x辆，根据题意可得50x-30（10-x）=260，解得x=7。因此，本题答案为D。

45. 工程队计划150天完成建筑，现计划30天后新增设备，提高20%工作效率，可以提前几天完成？（ ）
A. 20
B. 25
C. 30
D. 45

解析： 赋值“未提高之前的工作效率”为“1”，工作总量=工作效率×工作时间=1×150=150，按原工作效率工作的总量是：1×30=30，则剩余工作总量 是：150-30=120；提高后的工作效率是：1×120%=1.2，完成剩余工作总量需要的天数：120÷1.2=100（天）；可提前完成的天数= 计划天数-实际天数=150-（100+30）=20（天），因此，本题答案为A。

8、在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲，和L形区域乙、丙。已知三块区域甲、乙、丙的周长之比为4∶5∶7，并且区域丙的面积为48，求大正方形的面积（ ）。

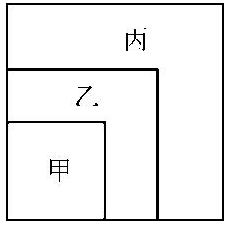
A. 96
B. 98
C. 200
D. 102

解析： 由于乙和丙是“L型区域”为非规则图形，我们采用“平移”思想。乙的周长等于中正方形的周长，丙的周长等于大正方形的周长，由题干“甲、乙、丙的周长之比 为4∶5∶7”可得，小、中、大正方形的周长之比为4∶5∶7，则小、中、大正方形的面积之比为16:25:49。我们设大正方形面积为49a，则中正方 形为25a，从而得到丙的面积为49a-25a=24a，题目已知“区域丙的面积为48”，故24a=48得到a=2，则大正方形的面积为 49a=49×2=98，因此，本题答案为B。

9、一个长方形周长130厘米，如果它的宽增加1/5，长减少1/8，就得到一个相同周长的新长方形，则原长方形的面积为（ ）平方厘米。
A. 1000
B. 900
C. 850
D. 840

解析： 假设长方形的长和宽分别为x，y，则有周长公式 的：2×（x+y）=130，又：改变之后周长相同，即宽增加的长度：y/5与长减少的长度：x/8相等，得出：y/5=x/8，联立两个方程解 得：x=40，y=25，易知长方形面积为：S=x×y=1000，因此，本题答案为A。

10、举办排球比赛，选男员工的1/11和12名女员工，剩余男员工是剩余女员工的2倍，总员工人数156人，问：男员工有多少人？（ ）
A. 100
B. 99
C. 111
D. 121

解析： 方法一：选出男员工的1/11，可知男员工的数量为11的倍数，首先排除 A，C，将B代入，得选出的男员工为9人，剩余90（剩余男员工数量），又：女员工数量为：156-99=57人，选出12人，剩余45人（剩余女员工数 量），90÷45=2，即：剩余男员工是剩余女员工的2倍，正好满足题意，直接锁定答案B。 方法二：此题亦可用方程思想解答：设男员工数量为x，则有（1-1/10）x=2×（156-x-12），解得x=99，所以男员工数量为99，因此，本题答案为B。