行测真题之数量关系典型例题精讲（12）

1. M、N两地之间要架设电缆，已知两地间地势复杂，电缆的架设需要绕道，绕道线路和相应的线路会导致的电量损耗（即所示数字，单位略）见下图。则从M到N架设电缆的电量耗损最低（ ）。

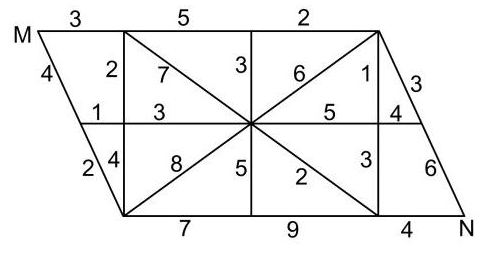
A. 14
B. 16
C. 17
D. 18

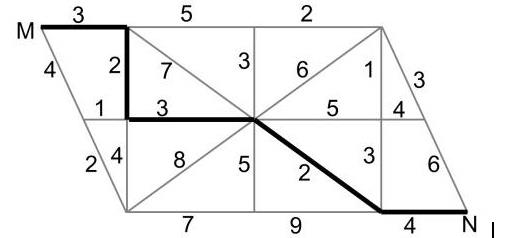
解析： 本题考查统筹问题。如图可得：从M到N架设电缆的电量耗损最低为4+1+3+2+4=14。故答案为A。


2. 某次会议需要印刷制会议材料，参会人员共计300人，每人发放一份会议议程，每5人公用一份会议讨论资料，每间客房（每间住2人，无单人）发放一份本地出行提示。会议材料的印刷价格如下，则印制会议材料一共需要花费（ ）元。

A. 3390
B. 3875
C. 4155
D. 5430

解析： 本题考查经济问题。依题可得印制会议材料一共需要花费：300×5+23×（300/5）+8.5×（300/2） =1500+1380+1275=4155。故答案为C。

3. 小李用几天时间看完了一本400页的书，第一天看30页，然后每天比前一天多看20页。在小李看书这几天的前半段时间（按整天计算），小李一共看了（ ）页。
A. 130
B. 150
C. 170
D. 190

解析： 本题属于计算问题。由于不确定最后一天看多少页，而且数字不大，可以用枚举法： 30，50，70，90，110，50相加即为400，即6天可以看完，那前半段时间也就是前3天共看了30+50+70=150页。故答案为B。

4. 某水果店销售一批水果，按原价出售，利润率为25%。后来按原价的九折销售，结果每天的销售量比降价前增加了1.5倍。责打折后每天销售这批水果的利润比打折前增加了（ ）。
A. 15%
B. 20%
C. 25%
D. 30%

解析： 本题属于经济问题。题中已知数据较少，比值较多时，为了便于计算可用假设法。设水果进价为100元，个数为2个，则原价为100×125%=125元，九 折后为125×0.9=112.5，销量为2+3=5个。打折前的利润为 25×2=50，打折后的利润为12.5×5=62.5，比打折前增加了（62.5-50）÷50=25%。故答案为C。

5. 某晚会计划设置抽奖环节，能用于购买奖品的总金额固定，且要求每名一等奖奖品的金额是二等奖的两倍，每名二等奖奖品的金额是三等奖的两倍。如果一、二、三 等级各设置两名，则一等奖奖品金额为每名720元。若一等奖设一名、二等奖两名、三等奖四名，则一等奖的奖品金额为每名（ ）元。
A. 780
B. 840
C. 880
D. 940

解析： 设三等奖的奖品金额为每名x元，则二等奖和一等奖的金额分别为2x和4x，若一等奖设一名、二等奖两名、三等奖四名，根据“总金额固定”可得：4x+2x×2+4x=720×2+360×2+180×2，解得x=210，4x=840。故答案为B

6. 某机构要派工作人员到9个乡镇进行业务检查。工作人员每到一个乡镇进行业务检查后必须返回单位汇报，这一行程的总时间见下表。如果这项工作要在16个小时内完成，则该单位至少要派出（ ）名业务。

A. 4
B. 5
C. 6
D. 7

解析： 本题考查统筹问题。总时间为2＋7＋8＋3＋11＋4＋6＋9＋14＝64，16小时内完成，不考虑其他细节，至少需要4个工作人员，此时要求每一组的时 间都为16小时。快速浏览表格，可知这一要求无法达到。因此考虑5个工作人员的情况，此时尽可能凑够16个小时，A＋D＋E，B＋C，F＋G，H，I就是 一种可能的情形。于是最少需要5名业务员。故答案为B。

7. 有8人进行围棋赛。第一轮比赛，8人随机组成4组对弈。之后每一轮比赛由前一轮比赛中所有获胜者随机组成2组对弈，所有失败者也随机组成2组对弈。则3轮比赛后，战绩为1胜2负的棋手最多有（ ）人。（本次围棋比赛没有和局）
A. 3
B. 2
C. 5
D. 4

解析： 依题意，第一轮：随机组成4组，则会出现4个人一胜，4个人一负的情况；第二轮：而获一胜的4人，再比赛，必出现2人二胜，2人一胜一负（前胜后负）的情 况。第三轮：二胜的2人和一负一胜（前负后胜）的两人再组合，最多的就是一负一胜的2人再输；二负的两人和一胜一负（前胜后负）的两人再组合，则最多的情 况就是一胜一负的再负，故最终一胜二负的最多为4人。故答案为D。

8. 公司安排6位新员工共同参加一次为期两天的活动，6个人围城一个圆桌进行交流。为促进新员工间的互动，如果要求第二天每个人身边坐着的两个人都与第一天不同，则新员工们有（ ）种座位安排方式。
A. 5
B. 6
C. 7
D. 8

解析： 本题考查排列组合问题。假定6个人编号为A、B、C、D、E、F，并第一天以此为序构成圆排列。第二天安排座位时，先安排A，那么其两侧只能安排C、D、 E三人中的2人，方法数A（3,2） ＝6。此三人一旦确定后，其余三人的安排方式是唯一固定的。因此最终安排座位方式共6种。故答案为B。

9. 甲公司的马经理从本公司坐车去乙公司洽谈，以30千米/时的速度出发20分钟后，马经理发现文件忘带了，便让司机以原来1.5倍的速度回甲公司拿，而他自己则以5千米/时的速度步行去乙公司。结果司机和马经理同时到达乙公司。甲乙两公司的距离是（ ）千米。
A. 12.5
B. 13
C. 13.5
D. 14

解析： 本题考查行程问题，司机返回时，走的路程是：30*（20/60）=10千米，那么，从马经理步行开始到两者同时到达乙时，司机比马经理多走了的路 程=2*10=20（可以画一个简单的示意图，很快就能看出两者之间的关系），那么设马经理的步行时间为x，可得：30*1.5*x-20=5x，解 得：x=0.5，那么S＝10+5*0.5=12.5（千米）。故答案为A。

10. 今年3月份的最后一天是星期六，则2013年3月份的最后一天是（ ）。
A. 星期天
B. 星期四
C. 星期五
D. 星期六

解析： 本题考查日期问题。从2012年3月31号到2013年3月31号，中间跨越一年，其中包括2013年的2月，而2013是闰年，因此这一年是365天，即52个星期多一天，所以2013年3月份的最后一天是星期六加一天，即星期天。故答案为A。

11. 某单位组织员工外出活动，所有员工刚好坐满10辆客车。已知大客车每辆乘坐50人，小客车每辆车坐30人，大客车比小客车一共多坐了260人。则大客车有（ ）辆。
A. 3
B. 4
C. 6
D. 7

解析： 本题比较简单，直接列方程求解。设大客车有x辆，依题可得：50x-30（10-x）=260，解得x=7。故答案为D。

12. 某公司去年有员工350人。与去年相比，今年本科及以上学历员工增加25人，本科以下学历员工减少了2%，总人数增加20人。则该公司今年本科及以上学历员工有（ ）人。
A. 75
B. 100
C. 125
D. 150

解析： 设今年本科及以上学历员工有x人，去年则为x-25，根据题意可得：[350-（x-25）]×2%=25-20，解得x=125。故答案为C。

13. 将一个表面积为18平方厘米的正方体沿对角线切成两块对称的三棱柱（见下图），并将这两块三棱柱重新拼接成一个大的三棱柱。则这个大三棱柱的表面积最大为（ ）平方厘米。