题目:
一正三角形小路如右图所示,甲乙两人从A点同时出发,朝不同方向沿小路散步,已知甲的速度是乙的2倍。问以下哪个坐标图能准确描述两人之间的直线距离与时间的关系(横轴为时间,纵轴为直线距离)?
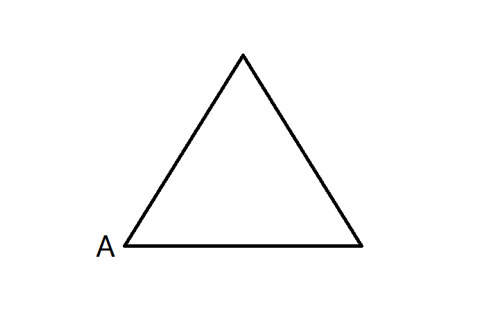
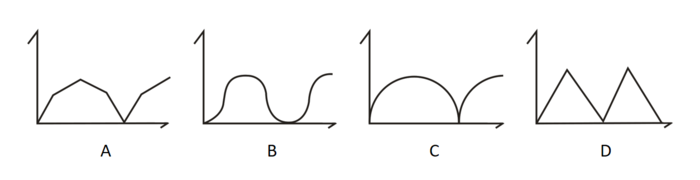
本题综合考查几何问题中的动点和函数图像。如图所示,当甲在AB段运动时,甲行驶的路程是乙的两倍,且已知图中三角形是正三角形,则∠BAC=60°,恰好满足甲、乙所在位置与A点构成直角三角形,根据解直角三角形,可得:S(甲乙之间的距离)=长直角边的长=√3 S(乙)= √3V(乙)*t。由于乙的速度不变,所以√3V(乙)是定值,S和t是线性关系。那么,首先排除B和C。再根据“甲移动到B点时,乙移动到AC中点,甲乙之间距离最大;甲移动到C点时,乙也移动到C点,两者之间距离为0”,只有D满足,故答案为D。

编辑:行测